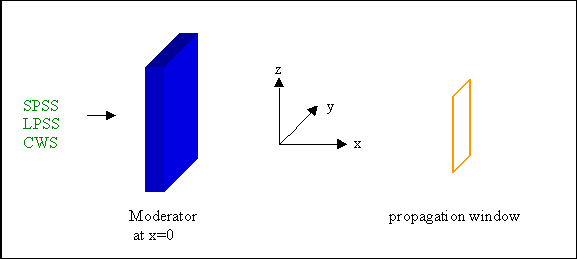
This module simulates also subsequent free propagation which can be limited in such a way, that only neutrons reaching a certain region of space are considered further on. The coordinate system is oriented as illustrated in the figure, it is centered in the middle of the moderator surface and shifted parallel to the x-axis to the position of the propagation window (i.e. the x-coordinate of each neutron which hit the propagation window is zero).

Every trajectory represents a package of a certain number of neutrons passing
per time, i.e. a certain neutron current. The sum over all trajectories gives
the total neutron count rate. From one module to the following, the 'number
of trajectories' decreases, e.g. if a window or the sample is not hit.
The intensity further decreases by reflections or absorption inside a material.
In these cases the number of trajectories is unchanged, but the count rate
per trajectory is decreased. So absolute values of the count rate are given
at any point of the instrument, if the moderator count rate can be determined.
As a consequence, the number of neutrons leaving one module (or
arriving on the detector) will be calculated, if the 'time of measurement'
is given. If the 'desired wavelength' is given, the optimal phases
of the disc choppers are calculated and written to the file 'instrument.inf'.
To enable ray-tracing, the 'ray-tracing file' has to be given
here and the 'kind of ray-tracing' has to be chosen. The ray-tracing
file contains the IDs of the trajectories to be traced. The 2 different
modes of ray-tracing are explained in a special help file called 'Ray-tracing'.
| Parameter Unit |
CWS |
SPSS |
LPSS |
Description | Range or values |
| pulse repetition rate [Hz] |
--- |
X |
X |
repetition rate of pulsed sources | > 0.0 |
| proton pulse length [ms] |
--- |
--- |
X |
proton pulse length of long pulse source | > 0.0 |
| special source |
--- |
X |
X |
Name of a neutron source, for which analytical functions are implemented to describe the moderator characteristics | "ESS", "SNS" |
| source name |
source name |
temperature | distr. files |
tau1, tau2 |
width, height | total flux | pulse rep. rate | pulse length of LPSS |
flux distribution |
| ESS | ESS | from input 50 or 325 K |
- - |
fixed |
from input (12x12cm²) |
calculated | from input (50 Hz) |
from input (2 ms) |
analytical funct. |
| SNS | SNS | from input 50 or 325 K |
- - |
fixed |
from input (12x12cm²) |
calculated | from input (50 Hz) |
--- | analytical funct. |
| continuous src. | - |
from input | - |
--- |
from input (12x12cm²) |
from input | --- | --- | Maxwell. distr. |
| continuous src. | - |
- | wavelength |
--- |
from input (12x12cm²) |
calculated | --- | --- | wavelength distr. file |
| pulsed src | - |
from input | - - |
from input (12 us; 60 us) |
from input (12x12cm²) |
from input |
from input (50 Hz) |
from input (2 ms) |
Maxwell. distr. function
time distr. function |
| pulsed src |
- |
- |
wavelength - |
from input (12 us; 60 us) |
from input (12x12cm²) |
calculated |
from input (50 Hz) |
from input (2 ms) |
wavelength distr. file
time distr. function |
| pulsed src |
- |
from input |
- time |
- |
from input (12x12cm²) |
from input |
from input (50 Hz) |
from input (2 ms) |
Maxwell. distr. function time distr. file |
| pulsed src | - |
- | wavelength time |
- |
from input (12x12cm²) |
calculated | from input (50 Hz) |
from input (2 ms) |
wavelength distr. file time distr. file |
| pulsed src |
- |
- |
wavelength-time |
- |
from input (12x12cm²) |
calculated |
from input (50 Hz) |
from input (2 ms) |
wavelength-time distr.
fct. |
1. Moderator Characteristics by Analytical Functions
For a reactor source, the Maxwellian distribution function can be used to describe the wavelength dependence of the neutron flux:
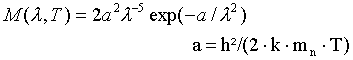
Therefore, the temperature has to be given. It is only used, if no 'wavelength distribution file' is given.
For a pulsed source, this wavelength dependence (or the 'wavelength distribution function' read from file) can be multiplied by a time dependent function F(t). For SPSS and LPSS we use:
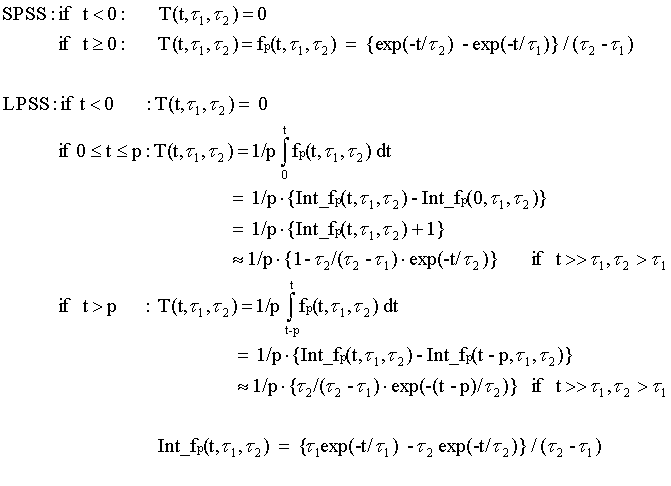
The parameters determining the pulse shapes must be given as an input. The second time constant describes the decay of the pulse, whereas both describe the shape in the beginning of the pulse. The length of the long pulse is determined by the proton pulse length. The decay is comparable to that of the short pulse. These functions are only used, if no 'time distribution file' is given.
ESS and SNS
2. Moderator Characteristics from Files
Alternatively the moderator characteristics can be given in files. Instead of giving the temperature, a 'wavelength distribution function' can be read. Instead of giving the time constants, a 'time distribution function' can be read. Both can be substituted at the same time by a 'wavelength-time distribution function'.
CW
For reactor sources, the so-called 'wavelength distribution function'
is needed. This file must contain a table of 2 columns. In the first column
the wavelength in Angstroem is expected, in the second the flux in flux
units (FU), i.e. n/(cm² s Ang str). The first column must have increasing
values. The wavelength range that can be used must be covered by the
range in this file.
From these data the 'total flux at the moderator' and the current
into a solid angle W are calculated:
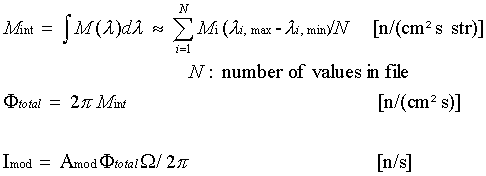
If the 'total flux at moderator' Ftotal is given, it is assumed that this is the real value and thus the data of the file are normalised to that value. If the 'neutron current' Imod is given, the flux is normalized to that value. This is only sensible, if the calculated current is zero, i.e. if area Amod, solid angle or wavelength range are zero.
SPSS/LPSS
For a pulsed source, the wavelength dependence of the intensity
can be determined by a given 'wavelength distribution function'
as in the CW case. Additionally, the time dependence of the flux can be
determined by a 'time distribution function'. It describes the time dependence
of the pulse. In the first column the time [ms] has to be given, in the
second the amplitude of the flux. The product of the amplitude given in
the wavelength distribution and that given in the time distribution must
have the unit n/(cm² s Ang str).
It is also possible to read a 2-dimensional file containing F(l,t). In the first row the wavelength values (in Angstroem)
are expected. All following have the time (in ms) in the first column
followed by flux values (in FU) for all wavelengths - see examples 'FluxLmbdTime.dat'
or files in 'IsisModData'. (Comment lines starting with '#' are allowed.)
In this approach of F(l,t) being the
product of the wavelength and the time distribution function, one gets
the following equations to determine the time averaged total flux and
the time averaged current into a solid angle W
is:
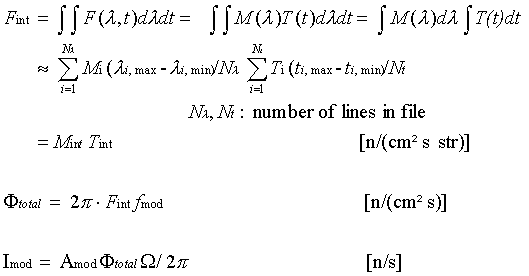
A simple rectangular or even instantaneous pulse can be generated
by using the CWS module and restricting the time window (see neutron parameters)
to the according range or to 0, respectively.
| Parameter Unit |
CWS |
SPSS |
LPSS |
Description | Range or values |
| moderator type |
X |
X |
X |
type of moderator, important for 'special sources'
(0: unknown or not important, 1: decoupled poisoned, 2: decoupled unpoisoned 3: coupled, 4: multi-spectral) Multi-spectral moderators consist of 2 or more parts, e.g. a cold and a thermal moderator, giving an effective flux distribution from the whole moderator, which is achieved by a special beam extraction system that is able to add the short wavelength distribution of the thermal moderator and the long wavelength distribution of the cold moderator (see F. Mezei: "Instrumentation Concepts" in "The ESS project Volume II", ed. D. Richter, 2002). The effective flux distribution was published by F. Mezei in Feb. 2002 as an email to the members of the ESS Instrumentation Task Group. This moderator can be used for simulations of instruments at ESS and SNS. |
0 - 4 |
| moderator shape |
X |
X |
X |
shape of the moderator: 0: rectangular,
1: circular |
0, 1 |
| wavelength distr. file |
X |
X |
X |
file describing the wavelength dependence
of the intensity (see also text) If the 'wavelength distribution file' is given, the temperature is not used. . |
|
| time distribution file |
--- |
X |
X |
file describing the time dependence of the
intensity (see also text) If the 'time distribution file' is given, the relaxation times and the pulse length are not used |
|
| wavelength-time distr. file |
--- |
X |
X |
file describing the wavelength and time
dependence of the intensity (see also text above) If the 'wavelength-time distribution file' is given, the relaxation times, the pulse length, and the temperature are not used |
|
| moder. temperature [K] |
X |
X |
X |
moderator temperature only used, if neither 'wavelength-time distribution file' nor 'wavelength distribution file' are given. |
> 0.0 |
| moder. width or diameter [cm] |
X |
X |
X |
rectangular moderator: bordered by center_y
± mod.width/2 in y-direction (see also last row) circular moderator : diameter of
the moderator
|
> 0.0 |
| moderator height [cm] |
X |
X |
X |
rectangular moderator: bordered by center_z
± mod.height/2 in z-direction (see also last row) circular moderator : not used |
> 0.0 |
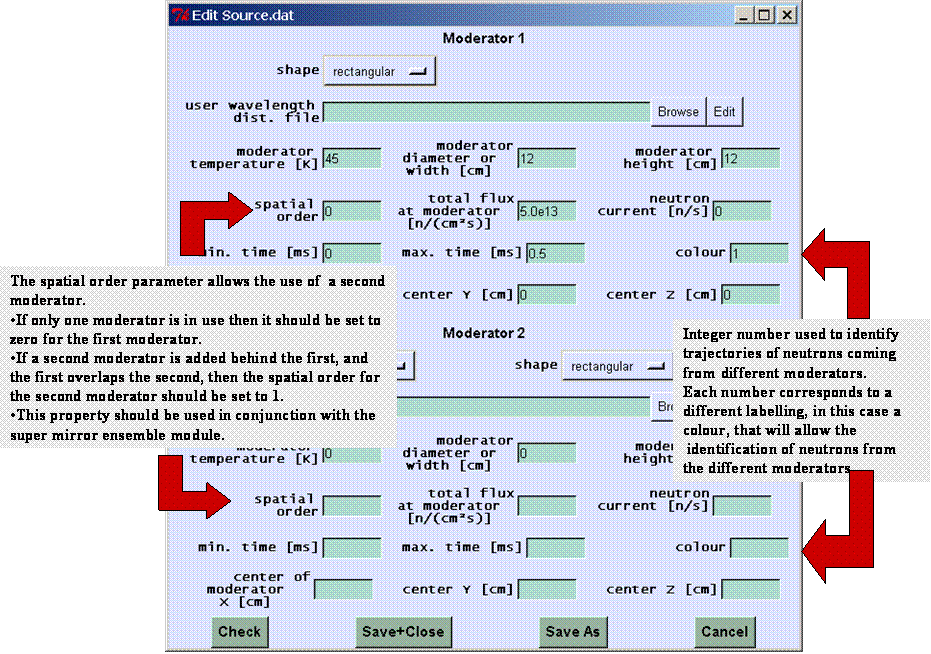
| spatial order |
X |
X |
X |
see following picture |
|
| total flux at moderat. [n/(cm²s)] |
X |
X |
X |
Flux on moderator surface into solid angle
2*pi integrated over the whole wavelength range ([0, infinity] for analytical
functions or total range given in distributions file) assuming an isotropic
flux distribution over 2*pi. It is sensible to give this value, if a Maxwellian distribution determined by the temperature is used, because this distribution is normalized to given an integral of 1. If a 'wavelength distribution file' or a 'wavelength-time distribution file' is used, it is straightforward to use a file with realistic flux values and to omit this value. But if it is given, it is assumed to be the correct value and thus the data of the file are normalised to give this total flux value. |
> 0.0 |
| neutron current [n/s] |
X |
X |
X |
Count rate leaving the moderator into the
chosen solid angle, integrated over moderator area and chosen wavelength
range. If the 'neutron current' is given, the flux is normalized to that value. This is only sensible, if the calculated current is zero, i.e. if moderator area, solid angle or wavelength range are zero. |
> 0.0 |
| tau_1 tau_2 [ms] |
--- |
X |
X |
time constant of the pulse shape (of pulsed
sources): tau_2 describes the decay of the pulse, whereas both describe the shape in the beginning of the pulse (see equations for pulsed sources above). |
> 0.0 > 0.0 |
| colour |
X |
X |
X |
see following picture |
0 - 32767 |
| center of moderator X Y Z [cm], [cm], [cm] |
X |
X |
X |
position of the moderator center - default:
(0.0, 0.0, 0.0) necessary to describe the arrangement of two (or three) moderators |
no restriction |
| Paramter Unit |
Description |
Range or Values |
Command Option |
| min. wavelength, max. wavelength [Å] |
minimal and maximal wavelength used in the simulation
|
>= 0 |
-m, -M |
| min. time, max. time [ms] |
pulsed sources: time range of the pulse
(as considered in the simulations) continuous source: usually min. time = max. time = 0.0, i.e. all neutrons starting at the same time. Otherwise a rectangular pulse is generated, which is e.g. necessary for time-of-flight instruments at continuous sources |
no restriction |
-t -T |
| max. diverg. x <-> y max. diverg
x <-> z [deg] |
The horizontal divergence phi (see figure below)
is chosen in the interval [-max.div x - y , +max.div x - y] The vertical divergence theta (see figure below) is chosen in the interval [-max.div x - z , +max.div x -z] |
0 ... 90 0 ... 90 |
-y -z |
| direction defined |
The direction is usually determined by a Monte Carlo
choice of phi and theta between the maximal values as given by the
user. Alternatively, the direction can be determined by the starting
point on the moderator surface, which is determined by other MC choices,
and a point on the propagation window (see below). |
by divergence by window |
-d |
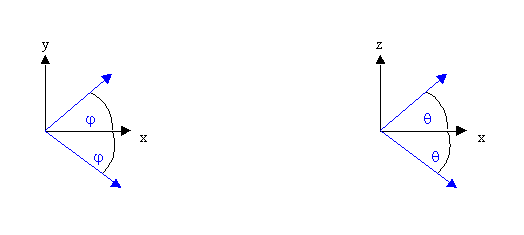
For both ways to restrict the divergence (by window and by max. angles),
the solid angle corresponding to the divergence window is calculated,
in order to determine absolute flux values. For every trajectory,
the count rate that it represents has to be calculated. If we have chosen
an analytic function to describe the moderator (e.g. the Maxwellian distribution),
we just use that value of M(l), T(t) or F(l,t) in the equation.
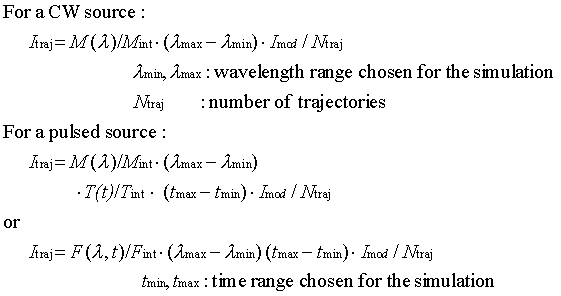
If the distribution files are used, M(l) or T(t) are interpolated in logarithmic scale, e.g.
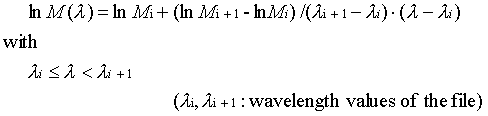
The polarization of the neutron beam is needed in some test computations.
Therefore an "internal" polarizer is defined in the source module. Initial
values of the percentage and the direction of polarization have
to be given. The spin vector belonging to each trajectory is represented
in cartesian coordinates. The output represents an ansamble of "Up" and
"Down" neutrons relative to the given direction of polarization. The average
polarization will be that given by the input parameter "degree of polarization".
For non-polarized beam (0%) the numbers of "Up" and "Down" trajectories are
the same.
Last modified: Tuesday, 03-Jul-2007 16:14:09 CEST